Vertical Oval Tank Volume Calculation

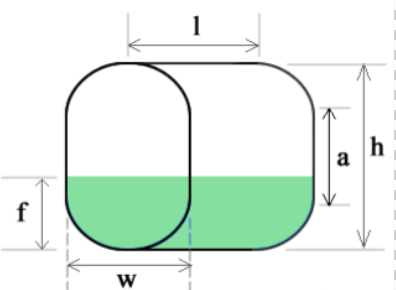
To calculate the volume of an oval tank, you first need to determine the area, A, of the end, which resembles a stadium shape, and then multiply it by the length, l. The formula for the area A is given by:

A = πr² + 2ra

However, the provided definitions for r and a seem to contain errors. Typically, for an oval tank with semicircular ends:

• r would be the radius of the semicircle (half the diameter of the circular end).
• a would represent the straight sides of the stadium shape.

Correctly, we should have:

• r = w / 2 (radius is half of the width of the circular end)
• a is some value related to the height and width, but not h - w.

Given the typical design of oval tanks, a is often derived from the overall dimensions of the tank but not directly as h - w. However, for the sake of this explanation and assuming a simplified design where the straight sides connect the semicircles at the top and bottom, we might approximate a as the difference between the height and the diameter of the semicircle (which is w), but this is not a standard definition.

Nevertheless, using the provided formula (with caution about the accuracy of r and a definitions):

V_tank = (πr² + 2ra)*l

Calculating the Fill Volume of a Vertical Oval Tank

It is helpful to envision the tank as two halves of a cylinder separated by a rectangular tank. Here’s how to approach the fill volume calculation based on the fill height f:

• Fill, f < r: Calculate the fill volume using the circular segment method, considering the filled portion as in a vertical cylinder tank.
• Fill, r ≤ f < (r + a): The filled volume consists of half of the cylinder portion up to height r (which is a full semicircle) plus the volume of the rectangular portion extending from r to f.
• Fill, (r + a) ≤ f < h: In this case, the tank is mostly filled, with the semicylindrical ends completely filled and some additional fill in the rectangular middle section. However, if we are calculating the remaining empty volume (as mentioned in your text), it would be V_{tank} - V_{filled}, where V_{filled} is the sum of the volumes of the semicylindrical ends and the rectangular section up to height f. Alternatively, directly calculate the filled volume using circular segment methods for the top empty segment if needed.