Oblique Cone Bottom Tank Volume Calculator

Tank Volume (m³):

Filled Volume (m³):

Tank Volume (U.S. Gallons):

Filled Volume (U.S. Gallons):

Tank Volume (Imp. Gallons):

Filled Volume (Imp. Gallons):

Tank Volume (Liters):

Filled Volume (Liters):

Tank Volume (Cubic Feet):

Filled Volume (Cubic Feet):

Tank Volume (bbl):

Filled Volume (bbl):

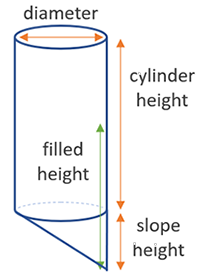
Oblique Cone Bottom Tank Volume Formula

Volume Calculation

The volume of an oblique cone bottom tank is calculated by determining the volume of the cylindrical section and the conical section. The total volume is given by:

\[ V_{\text{slope}} = \frac{1}{3} \pi r^2 H_{\text{slope}} \]

Where:

r = radius (diameter / 2)
H_slope = height of the slope section

\[ V_{\text{cylinder}} = \pi r^2 H_{\text{cyl}} \]

Where:

r = radius (diameter / 2)
H_cyl = height of the cylindrical section

The total volume of the tank is the sum of the volumes of the cylindrical and conical sections:

\[ V_{\text{tank}} = V_{\text{cylinder}} + V_{\text{slope}} \]

Filled Volume Calculation

The filled volume of the tank is calculated using the formula:

If filled height is less than or equal to slope height:

\[ V_{\text{filled}} = \frac{1}{3} \pi \left(\frac{H_{\text{filled}}}{H_{\text{slope}}}\right) r \left(\frac{H_{\text{filled}}}{H_{\text{slope}}}\right) r H_{\text{filled}} \]

If filled height is greater than slope height:

\[ V_{\text{filled}} = \pi r^2 H_{\text{filled}} + V_{\text{slope}} \]

Where:

H_filled = filled height
H_slope = height of the slope section
r = radius (diameter / 2)