Horizontal Cylinder Tank Volume Calculator

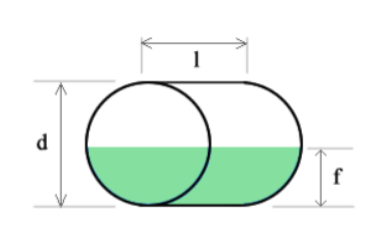
Total Volume (m³):

Filled Volume (m³):

Total Volume (U.S. Gallons):

Filled Volume (U.S. Gallons):

Total Volume (Imp. Gallons):

Filled Volume (Imp. Gallons):

Total Volume (Liters):

Filled Volume (Liters):

Total Volume (Cubic Feet):

Filled Volume (Cubic Feet):

Tank Volume (bbl):

Filled Volume (bbl):

Total Volume of the Horizontal Cylinder Tank

The total volume \( V_{\text{tank}} \) of a cylinder-shaped tank is determined by multiplying the area \( A \) of its circular end by its length \( l \). The area \( A \) of the circular end is given by \( \pi r^2 \), where \( r \) is the radius, which is equal to half the diameter or \( \frac{d}{2} \). Thus, the total volume of the tank is:

\( V_{\text{tank}} = \pi r^2 l \) Filled Volume of a Horizontal Cylinder Tank

To calculate the filled volume of a horizontal cylinder tank, we first need to find the area \( A \) of the circular segment that corresponds to the filled portion and then multiply it by the length \( l \).

For a circular segment, the shaded area \( A \) is given by:

\( A = \frac{1}{2} r^2 (\theta - \sin\theta) \)

where \( \theta \) is in radians and is calculated as:

\( \theta = 2 \arccos\left(\frac{r}{m}\right) \)

Here, \( m \) represents the vertical distance from the center of the circle to the chord defining the segment's base.

Thus, the volume of the circular segment \( V_{\text{segment}} \) is:

\( V_{\text{segment}} = \frac{1}{2} r^2 (\theta - \sin\theta) l \)

Case 1: Fill Height Less Than Half the Diameter

If the fill height \( f \) is less than half the diameter \( d \) (i.e., \( f < \frac{d}{2} \)), we use the segment created by the filled height directly, and the filled volume \( V_{\text{fill}} \) is:

\( V_{\text{fill}} = V_{\text{segment}} \)

Case 2: Fill Height Greater Than Half the Diameter

However, if the fill height \( f \) is greater than half the diameter \( d \) (i.e., \( f > \frac{d}{2} \)), we need to calculate the segment corresponding to the empty portion of the tank and subtract it from the total volume to get the filled volume. In this case:

\( V_{\text{fill}} = V_{\text{tank}} - V_{\text{segment}} \)

where \( V_{\text{segment}} \) now represents the volume of the empty segment.