Dome Roof Cone Volume Calculator
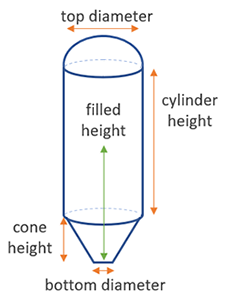
Dome Roof Cone Tank Volume Formula
Volume Calculation
The volume of a dome top cone tank is calculated by determining the volume of the cylindrical section, the conical section, and the dome section. The total volume is given by:
\[ V_{\text{cylinder}} = \pi r^2 H_{\text{cyl}} \]
Where:
- r = top radius (top diameter / 2)
- Hcyl = height of the cylindrical section
$$ \text{Cone Volume} = \frac{\pi}{3} \cdot \text{cone height} \cdot (br^2 + br \cdot tr + tr^2) $$
Where:
- Hcone = height of the conical section
- Dinf = bottom diameter
- Dsup = top diameter
\[ V_{\text{dome}} = \frac{2}{3} \pi r^3 \]
Where:
- r = bottom radius (bottom diameter / 2)
The total volume of the tank is the sum of the volumes of the cylindrical, conical, and dome sections:
\[ V_{\text{tank}} = V_{\text{cylinder}} + V_{\text{cone}} + V_{\text{dome}} \]
The filled volume of the tank is calculated using the formula:
If filled height equals cone height:
$$ \text{Filled Volume} = \frac{\pi}{3} \cdot \text{cone height} \cdot (br^2 + br \cdot tr + tr^2) $$
If filled height is greater than cone height:
$$ \text{Filled Volume} = \frac{\pi}{3} \cdot \text{cone height} \cdot (br^2 + br \cdot tr + tr^2) + \pi \cdot tr^2 \cdot (\text{filled height} - \text{cone height}) $$
If filled height is less than cone height:
$$ R_{\text{cut}} = br + \left(\frac{\text{filled height}}{\text{cone height}}\right) \cdot \text{cone height} \cdot \left(\frac{tr - br}{\text{cone height}}\right) $$ $$ \text{Filled Volume} = \frac{\pi}{3} \cdot \left(\frac{\text{filled height}}{\text{cone height}}\right) \cdot \text{cone height} \cdot \left(br^2 + br \cdot R_{\text{cut}} + R_{\text{cut}}^2\right) $$
Where:
- r = top radius (top diameter / 2)
- Hfilled = filled height
- Hcone = height of the conical section
- Dinf = bottom diameter
- Dsup = top diameter
 Home
Home Back
Back